Echilibrul relaţiilor, mecanicã statisticã, jocuri, statut social: o aventurã interdisciplinarã (II)

In episodul trecut v-am fãcut cunoştinţã cu dinamica triadicã introdusã de Antal, Krapivsky şi Redner, şi cu tranziţia ei de fazã. Probabil cã nu v-a scãpat faptul cã modelul presupunea („toate vacile sunt sferice”) o structurã nerezonabilã a societãţii: toatã lumea se cunoaşte cu toatã lumea, şi toate triadele sunt la fel de importante.

Antal, Krapivsky şi Redner au intrebat ce se intâmplã dacã in locul unui graf complet considerãm unul oarecare? E o problemã pe care am inceput s-o inţeleg intrucâtva, pentru cã am publicat un articol despre acest model. Nu e vorba de tranziţii de fazã (nu sunt fizician), ci de rezultate matematice. Cu ingãduinţa voastrã vã voi povesti câte ceva despre rezultatele din acest articol – keep in mind, problemele rãmase deschise sunt mai numeroase decât cele pe care le-am rezolvat …

Transformând problema prin dualitate

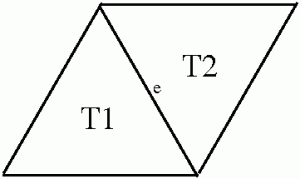
Punctul meu de plecare a fost un alt fel de a privi problema numit dualitate. Sã considerãm douã triunghiuri care au in comun o muchie pe care o vom numi .

Ce se intâmplã dacã triada este aleasã in dinamica constrânsã şi, mai mult, muchia este cea care işi schimbã semnul ?

Evident triunghiul devine echilibrat (el era neechilibrat inainte; ştim asta pentru cã a fost triunghiul ales). Pe de altã parte modificarea are un efect cuantificabil asupra lui deasemenea: dacã inainte era neechilibrat va deveni, de asemenea, echilibrat; dacã inainte era echilibrat va deveni neechilibrat.

Evident, mai multe triade pot impãrţi muchia cu , dar e posibil şi sã nu fie niciun alt triunghi. Vom inventa un fel „dual” de a vedea dinamica descrisã mai sus: creãm un hipergraf asociat grafului . Vârfurile lui corespund triunghiurilor lui . Pe de altã parte vom pune o hipermuchie in pentru fiecare muchie in . Ea uneşte vârfurile in (triunghiuri in ) care conţin muchia .

Un exemplu: sã considerãm un graf care poate fi descris drept un „cerc de triunghiuri”:

Mai jos desenãm „dualul” sãu . Vã rog sã observaţi cã fiecare vârf al lui are câte un mic ciclu: o hipermuchie cu un singur vârf. Asta pentru cã fiecare triunghi in are câte o muchie care nu apare in niciun alt triunghi.

Cum descriem dinamica pe 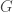cu ajutorul lui ?

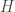Simplu: vedem triunghiurile neechilibrate in ca nişte „bile” aşezate pe vârful corespunzãtor triunghiului in . La fiecare pas:

1. alegem la intâmplare o bilã b („un triunghi t neechilibrat in G”)
2. alegem la intâmplare o hipermuchie e care conţine bila respectivã („o muchie m a lui t cãreia urmeazã sã ii schimbãm semnul”)
3. ştergem bila b. Adãugãm o bilã in fiecare vârf al lui e care nu conţinea una. Stergem orice bilã din vârfurile lui e care conţineau o bilã inainte („efectul schimbãrii semnului muchiei m”)

Dacã hipergraful ar fi de fapt un graf am putea vedea procesul de mai sus intr-un fel foarte intuitiv: alegem o bilã la intâmplare şi o mutãm intr-un vecin aleator ales. Douã bile care se intâlnesc se ciocnesc („anihileazã”).

Procesul pe care tocmai l-am descris e binecunoscut in domeniul sistemelor interactive de particule şi poartã un nume special in englezã: annihilating random walk. El a fost studiat indelung, ce-i drept mai ales in latici infinite, dar existã câteva rezultate şi pentru grafuri finite (vezi aici).

Deocamdatã noul fel de a vedea problema ne permite sã inţelegem ce se intâmplã in exemplul de mai sus:  o particulã se poate „autoanihila” dacã hipermuchia aleasã e ciclul adiacent vârfului. Mai mult, in medie, fiecare particulã aleasã se autodistruge la fiecare pas cu probabilitate constantã (de exemplu 1/3 când muchia e aleasã uniform la intâmplare). Prin urmare:

• starea finalã nu mai conţine triunghiuri neechilibrate.
• o asemenea stare se atinge (in medie) intr-un timp liniar in numãrul de triunghiuri.

In cazul general, existenţa unei singure bucle intr-un conex este suficientã pentru a garanta cã in starea finalã toate triunghiurile sunt echilibrate (dual, nicio bilã nu supravieţuieşte in ): putem muta orice bilã in vârful care conţine bucla. Pe urmã folosim bucla pentru a o anihila.

Ce se intâmplã dacã este un graf conex care nu conţine bucle ? Evident, singura sursã de dispariţie a particulelor e anihilarea lor prin ciocnire. Cum particulele se anihileazã in perechi, paritatea numãrului iniţial de particule se pãstreazã, şi influenţeazã descrierea stãrii finale: dacã numãrul iniţial de particule era par, in starea finalã ele dispar toate. Daca era impar, atunci o singurã particulã supravieţuieşte.

In cazul ãsta putem sã rãspundem şi la urmãtoarea intrebare: de câţi paşi avem nevoie in medie, pornind din starea iniţialã cea mai defavorabilã pentru a atinge starea cu cel mult un triunghi neechilibrat (o singurã „bilã” in hipergraful dual) ?

Evident, raspunsul la intrebarea de mai sus depinde de structura lui ; mai precis de structura lui . Sã ne imaginãm cazul in care e impãrţit in douã jumãtãţi care „nu prea comunicã intre ele” şi douã bile, câte una in fiecare jumãtate. Evident, dinamicii ii va lua mult timp ca sã facã cele douã bile sã se intâlneascã.

Rezultatul pe care l-am demonstrat aratã cã, cel puţin in cazul in care este un graf fãrã bucle, acesta este intr-un anumit sens singurul obstacol pe care il poate pune in calea dinamicii.

Dacã (puţin probabil) aş avea cititori versaţi in teoria lanţurilor Markov cu amestecare rapidã, aceştia s-ar putea sã ştie cã fenomenul pe care l-am descris mai sus cuantificã de multe ori viteza de convergenţã a multor lanţuri Markov cãtre distribuţia staţionarã: cantitãţi precum conductanţa şi altele inrudite mãsoarã precis gradul in care putem „sparge” un graf in douã jumãtãţi slab conectate şi, deopotrivã, viteza de convergenţã a lanţurilor Markov (pentru experţi: cel puţin in cazul reversibil).

In cazul meu am redus problema la un rezultat cunoscut: timpul de convergenţã pentru o altã dinamicã, numitã mers aleator cu coalescenţã e mãrginit superior folosind o variantã a aşa-numitului timp Cheeger al unui graf.

Dar ce este un mers aleator cu coalescenţã ? Imaginaţi-vã din nou un numãr de bile care se mişcã aleator pe un graf. Când douã bile se intâlnesc, spre deosebire de cazul mersurilor aleatoare cu anihilare, particulele se „lipesc” intr-un cluster. Noi particule şi clustere continuã sã se lipeascã pânã când rãmâne un singur cluster de particule. Evenimentul de interes e prin urmare timpul pânã când rãmâne un singur cluster.

Bun, acest timp poate fi mãrginit superior (credeţi-mã pe cuvânt, sau citiţi din cartea lui Aldous şi Fill, capitolul 14) folosind timpul Cheeger. Ce legãturã are asta cu dinamica noastrã ? Rãspunsul este cã aceasta din urmã converge „mai rapid”. Pentru a vedea acest lucru vom rula mersul aleator cu coalescenţã şi vom reinterpreta anumite aspecte ale lui intr-un fel in care ne va permite sã il vedem drept o realizare a unui mers aleator cu anihilare. Tehnica e mult mai generalã, se numeşte cuplajul a douã variabile aleatoare (lanţuri Markov), dar in cazul acesta v-o pot explica intuitiv.

Particule vii, particule zombie şi timpul de convergenţã

Sã considerãm un mers aleator cu coalescenţã, doar ca bilele le vom clasifica in douã categorii: „vii” şi „zombie„. Toate bilele sunt intial „vii”. Pe de altã parte, când o bilã vie intâlneşte o alta, ambele se transformã in „bile zombie”. Particulele zombie se pot mişca in continuare, lipindu-se de o particulã vie, dacã o intâlnesc. Pe de altã parte orice cluster poate conţine cel mult o particulã vie.

Punctul crucial este urmãtorul: dacã privim dinamica unui mers aleator cu coalescenţã, doar cã doar bilele „vii” sunt vizibile, ea este aceeaşi cu un mers aleator cu anihilare !

De asemenea, sã presupunem cã pornim cu un numãr par de particule. Atunci la momentul când rãmâne un singur cluster toate particulele sunt deja zombie. Motivul e foarte clar: fiecare cluster conţine cel mult o particulã vie. Pe de altã parte particulele devin zombie in perechi.

Dar asta nu inseamnã altceva decât faptul cã timpul de convergenţã pentru annihilating random walk e mai mic sau egal decât timpul pentru coalescing random walk (incluzând „paşii invizibili”, fãcuţi de clusterele de particule zombie).

Dupã cum am spus acest ultim timp de convergenţã poate fi mãrginit superior folosind timpul Cheeger al grafului H. In mod remarcabil, se crede faptul cã aceastã margine are acelaşi ordin de mãrime cu marginea inferioarã, datã de timpul mediu necesar pentru ca douã bile sã se intâlneascã in H, calculat din cele mai dezavantajoase poziţii iniţiale.

De asemenea, o consecinţã simpaticã a acestui rezultat este cã putem obţine (teoretic – ar trebui sã calculãm constanta Cheeger, lucru nu foarte uşor) o expresie exactã pentru timpul de convergentã intr-un caz in care fizicienii au estimat acest timp cu mijloace experimentale.

Ce se intâmplã când H este un hipergraf  oarecare (nu graf) ?

In acest caz problema este mai dificilã: urmãtorul invariant era adevãrat in cazul unui graf, dar nu mai e valabil in general:

La fiecare pas numãrul de particule se menţine constant sau descreşte.

Aceastã proprietate intervenea explicit in demonstraţia bazatã pe constanta Cheeger. Faptul cã ea nu mai e adevãratã semnaleazã nevoia de a folosi metode mai sofisticate din teoria lanţurilor Markov cu amestecare rapidã. Unele rezultate mai simple (de exemplu natura stãrii finale) sunt in continuare valabile, insã deocamdatã nu am un rãspuns complet.

O promisiune pentru viitor: dinamica „balanţei sociale slabe”

Ce se intâmplã dacã „duşmanul duşmanului meu nu mi-e neapãrat prieten” ? Acest concept se numeşte balanţã socialã slabã, şi a fost studiat in literatura de specialitate (vezi de exemplu interesanta carte a lui Kleinberg şi Easley). Intrebarea de mai sus a fost pusã recent (februarie 2011) intr-un articol din PNAS. Am obţinut şi mai recent 🙂 câteva rezultate despre aceastã problemã – interesant, dinamica bazatã pe balanţã slabã pare sã conveargã mai rapid. Dar despre asta intr-un episod viitor :).